DingDing

幻方 (Magic square)

                     

早前在地鐵車廂中看到一名女士很努力在填寫數讀遊戲, 這令我想起年前威廉講解給我聽關於幻方的構造法.  這當然與數讀有很大分別, 但幻方的解構對我這個非數學生也感到很有趣, 希望能與大家分享... 

幻方(Magic Square)，有時又稱魔方，由一組排放在正方形中的整數組成，其每行、每列以及兩條對角線上的數之和均相等。
而世界上最早出現的魔方陣目前公認是出現在中國。 據說大禹治水時，在洛水發現一隻大烏龜，背上刻有圖案，若用數字表示 就是三階魔方陣，所以後來這種三階魔方陣就被稱做洛書。

   洛書 

奇數階幻方構造法

Siamese方法是構造奇數階幻方的一種方法，說明如下：

- 把1放置在第一行的中間。
- 順序將等數放在右上方格中。
- 當右上方格出界的時候，則由另一邊進入。
- 當右上方格中已經填有數，則把數填入正下方的方格中。
- 按照以上步驟直到填寫完所有N²個方格。 


 3X3 animation: http://grapevine.net.au/~grunwald/une/KLAs/maths/magic3x3.html

(由於幻方的對稱性，也可以把右上改為右下、左上以及左下等方位)

.....................
..........


然而奇數的幻方解法就如將上下與左右的邊沿同時連起成圓筒狀般:


  上下的邊沿同時連起成圓筒狀




左右的邊沿同時連起成圓筒狀





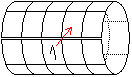
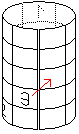
偶數階幻方構造法
4X4幻方構造法

對於4X4幻方一般都用對調法，製作起來很容易。如4階幻方的排列法：